The Ultimatum Game
- Uttkarsh Kohli

- May 30, 2020
- 4 min read
Updated: May 31, 2020
I have been learning Game Theory and I came across a very interesting game - The Ultimatum Game. I wanted to do the experiment in my school and see if the results are reciprocated. After voting, I asked a few friends the reasoning for their answer. Based on the answer, I explained the concept of high stake and low stake games and asked them the same question but with different stakes. I am going to conclude my results and try to match them with what I have learnt.
---------------------------------------------------------------------------------------------------------------------------
The ultimatum game is an experimental economics game in which two people interact anonymously and only once. The first player makes an offer of a share of their money.
If the second player accepts this offer, they receive according to the proposed offer.
If player 2 rejects the offer, neither gets anything.
The amount each player gets is called their 'pay-off' of the game.
Player 1 is given 10 pieces of Gold. They have to decide how much to offer to Player 2.
Lets say Player 1 offers x pieces, and the offer is accepted.
The pay off for Player 1 = 10-x.
The pay off for Player 2 = x.
A strategy profile is a set of strategies for all players which fully specifies all actions in a game. A strategy profile must include one and only one strategy for every player.
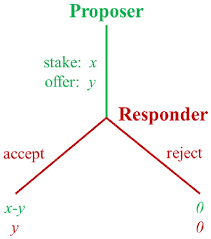
All possible actions in this game can be represented through a game tree.
The first node represents the various offers made by Player 1. Corresponding to the choice made by Player 1, Player 2 has 2 options at each node.
This is the strategy profile for the game:

A stands for accepting and R starts for rejecting.
The pay-offs are represented at the end nodes as (10-x , x) where x is the offer made by Player 1.
The theoretical description of the game:
The game assumes both players are rational and try to maximise their pay-offs.
Looking at the game through Player 1's perspective:
Player 1 knows that Player 2 is rational. Based on this, Player two should accept any offer greater than 0. If Player two rejects, they automatically get 0.
Since Player 1 knows he can make any offer , the theoretical offer should be 1 piece.
The pay-off for player 1 = 9 and pay-off for player 2 = 1.
Player 1 can offer 0 pieces as well, but since this offer makes the Player 2 indifferent in their choice, the offer may be rejected
Looking at the game through Player 2's perspective:
Since there is only one offer and no communication, Player 2's choices can be represented by the subgame which includes the choices of only the node Player 1 chooses.
Since Player 2 cannot threaten to reject an offer to make Player 1 offer a higher amount, Player 2 should theoretically accept any offer.
For each subgame, the subgame perfect equilibrium(The best choice that can be made or the choice for which no other choice gives a higher pay-off) is accept.
Results of my Experiment:
In the experiment, I made the participants Player 1.
This allowed me to make the participants value in risk of rejection of their offer.
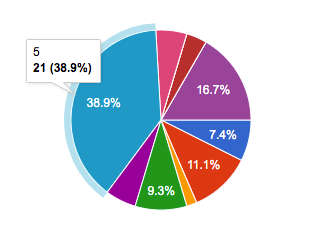
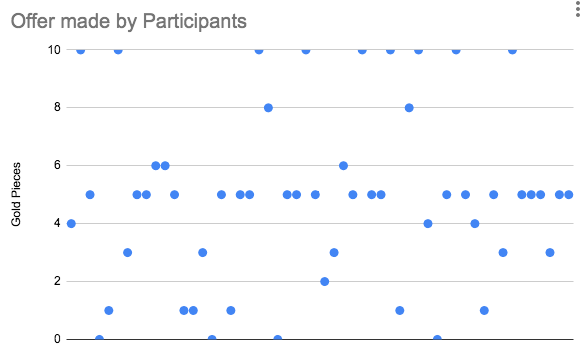
As it is visible, 38.9% of the participants choose to offer 5 and 63% above 5.
In reality, most people consider fairness while making an offer.
Less than 37% people offered to give less than 5 pieces and only 11% people offered 1.
These results may make one wonder, why do people want to offer more than necessary.
On talking to a few people, I realised that people tend to think of a situation through the receiving end. They think about what they would accept knowing what the other player is getting.
Instead of assuming the role of just Player 1, they think like they are Player 2.
Even then, they fail to realise that any offer is better than 0.
Most people compare their profit to that of the other player rather than valuing their profit compared to 0.
Some people went on to call Player 2 stupid if they accept anything lower than 5.
This thought completely disregards Player 2's aim for maximising their profit and shows that one is willing to accept a pay-off of 0 given that Player 1 is punished for offering unfairly.
Example of two people( Say C and S):
C and S are considered to be people valuing risk.
I asked C a low stake version of the game, and S a high stake version of the game.
Stake for C - 10 coins. Stake for S - 10 Million dollars.
C immediately said he would offer 5. The reasoning was as follows:
"Player 2 will reject any lower offer because they will think its unfair."
C valued fairness more than profit here due to the stake being very low and assuming the Player 2 can do without gaining anything that makes them feel the offer is fair.
S thought for a second and answered 1 Million. The reasoning was as follows:
"Player 2 will not reject the offer of a Million dollars for free just because I am getting more."
S realised that Player 2 would disregard fairness in order to get a pay-off of 1 Million dollars.
Conclusion*:
Fairness exceeds value of profit for small stakes for the majority of people.
People tend to value the feeling of receiving less than someone else more than receiving a lower profit.
This is very common, sometimes even when stakes are large and can be displayed through many other ways.
In fact it is a popular strategy in competing business's. Lowering ones own profits to minimise a rival companies profit.
Example:
Uber Eats, a food delivery platform offered extreme discounts even to the point of taking losses for a long period of time. Through this strategy, Uber Eats lowered the number of customers of other companies vastly. This forced the owners of other companies to sell their company to a bigger market share holder to get some profit while the company is on the verge of bankruptcy.
*[All statements made and reasoning for them are mine own and not professional views.]
Extra resources:
My Poll: https://forms.gle/NVAgQVvAs4NLQqhW7
Professional views about the results of Ultimatum Game: https://www.cs.mcgill.ca/~rwest/wikispeedia/wpcd/wp/u/Ultimatum_game.htm
Interesting variant of the game: The Ultimatum Game where on rejecting, Player receives a negative Pay-off.
More games to check out : prisoner's dilemma and the Battle of the sexes.
My sources:
Experiment with sample size of 53 people.
Sample size mostly consisted of 16-17 year high school students.



Comments