Chess and Mathematics
- Uttkarsh Kohli

- Feb 3, 2020
- 2 min read
Lately,I have gained interest in Chess and I have been playing a lot of it!
Since I am inclined towards the Mathematical side of everything I decided to search up and learn how Math can be used to become better at Chess.This is just a small reflection and examples of what I learnt. Hopefully this can get all of you excited about the game as well.
---------------------------------------------------------------------------------------------------------------------------
Chess is a game which is played all over the world. Almost 600 million people play it globally. Not only is chess enjoyable to play but it is also great for the development of one’s mind.
Learning chess helps to develop thinking skills, enhance mental prowess and directly contribute to improved academic performance and make people smarter in a variety of ways; for example, chess elevates one's ability to think rationally.
Chess and Math can be related to each other in several ways.
To name a few:
1)Chess promotes thinking skills of higher order.
2)Analysis of positions has a lot in common with mathematical problems.
3)Introduces a coordinates system.
4)Capacity to predict and anticipate consequences.
The final stage of a chess game - the endgame is very important.
Geometry plays a very important role.
Even during the Middle Ages, good chess players employed simple geometric rules to figure out, with a simple glance at the chess board, what would be the result of the encounter.
Let's look at an example: the famous “rule of the square.”
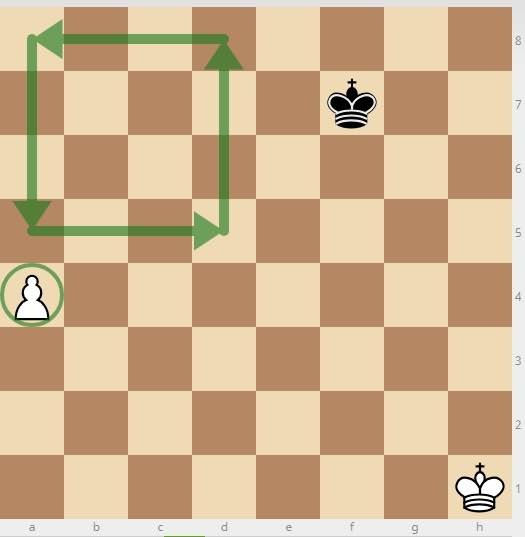
'Every pawn has its square when it going to be promoted. If a King is inside this area he will catch this pawn. If a King is outside this area he will not catch this pawn. Simple! I can show you how it works.
Here is the position.
Draw a diagonal from the pawn to the closest square to the king on the last rank and form a square.
This is a very elegant example of applying geometry in chess.
Next lets take a look at the The Eight Queens Puzzle.
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n = 2 and n = 3.
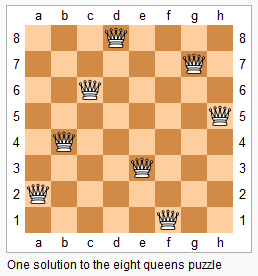
The eight queens puzzle has 92 distinct solutions. If solutions that differ only by the symmetry operations of rotation and reflection of the board are counted as one, the puzzle has 12 solutions.
These are called fundamental solutions
A fundamental solution usually has eight variants (including its original form) obtained by rotating 90, 180, or 270° and then reflecting each of the four rotational variants in a mirror in a fixed position.
If n > 1, it is not possible for a solution to be equivalent to its own reflection because that would require two queens to be facing each other.
These are just a few examples of how Chess and Math can be interrelated.



Comments