Inverse functions:
In brief, an inverse function is the opposite of any given function.
In mathematics, an inverse function (or anti-function) is a function that "reverses" another function.
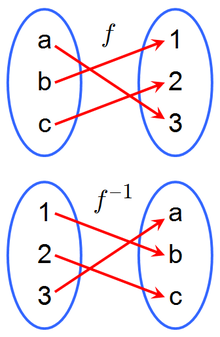
If the function f applied to an input x gives a result of y, then applying its inverse function
g to y gives the result x, and vice versa.
i.e., f(x) = y then f ^-1(y) = g(y) = x.
For example,
Let f(x) = x+3 = y ,
Then f ^-1(y) = y -3 = x . [Addition changes to Subtraction]
Let f(x) = 3x = y ,
Then f ^-1(y) = y /3 = x . [Multiplication changes to Division]
The domain Df becomes the range Rf^-1 for the inverse function and the range Rf becomes the domain Df^-1 .
Inverse Trigonometric functions
Tan(θ) = Opposite / Adjacent = y
By the definition of inverse functions,
Inverse tangent = arctan(y) = θ.
Trigonometric functions are periodic functions, thus inverse functions have multiple values for θ. In trigonometric functions, principal values are used.
Domain and Range of [Tan(θ) = Sin(θ)/Cos(θ)]
Tan(θ) is undefined at Cos(θ) = 0.
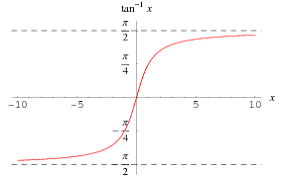
f(θ) = Tan(θ) = y
Df ∈ R - (2n+1)pi/2 , n ∈ Z.
Rf ∈ R
Let g(y) = f ^-1(y) = arctan(y) = θ
Dg ∈ R
Using principal values,
Rg ∈ (-pi/2, pi/2).
-pi/2 and pi/2 are not included as
Tan(-pi/2) and Tan (pi/2) are undefined.
Cot(θ) = Adjacent/Opposite = y
By the definition of inverse functions,
Invers cotangent = arccot(y) = θ.
=> arccot(y) = θ.
=> arccot(Adjacent/Opposite) = θ.
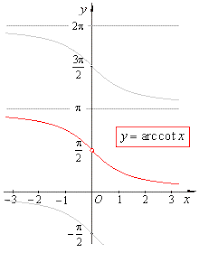
Domain and Range of [Cot(θ) = Cos(θ) / Sin(θ)]
Cot(θ) undefined at Sin(θ) = 0.
f(θ) = Tan(θ) = y
Df ∈ R - (n pi) , n ∈ Z.
Rf ∈ R
g(y) = f^ -1(y) = arccot(y) = θ
Dg ∈ R
Using principal values,
Rg ∈ (0 , pi).
0 and pi are not included as
Cot(0) and Cot (pi) are undefined.
Principal Value Range
The principal value of an inverse trigonometric function at a point x is the value of the inverse function at the point x , which lies in the range of the principal branch. For instance, the principal value of tan-1 (1) is 𝜋/4. Since 𝜋 /4 ∈ (-pi/2, pi/2).
As the period of tan(θ) is 𝜋, we can take any interval of length 𝜋 to be the principal range
If the interval contains a point of the form θ = (2n+1)𝜋/2, we have to deal with an asymptote as cos(θ) = 0 for θ = (2n+1)𝜋/2. Thus, to keep the function arctan(x) continuous on the principal branch, we take the range R ∈ (-pi/2, pi/2).
Similarly for cot(θ), we can take any interval of length 𝜋 to be the principal range .
If the interval contains a point of the form θ = (n)𝜋, we have to deal with an asymptote as sin(θ) = 0 for θ = (n)𝜋. Thus, to keep the function arccot(x) continuous on the principal branch, we take the range R ∈ (0, pi).
Some common values for arctan(x) and arccot(x):
Resources: