What are Mersenne Primes?
Discovered by and named after Marin Mersenne, Mersenne primes are prime numbers which are one less than a power of two. They were first studied by Mersenne in the 17th century.
In mathematical terms Mersenne primes may be denoted as primes of the form 2n - 1.
To further study Mersenne primes, look at this pattern-
21 - 1 = 1
22 - 1 = 3
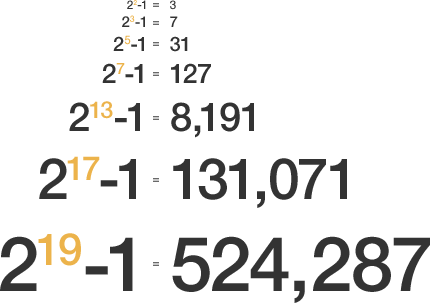
23 - 1 = 7
24 - 1 = 15
25 - 1 = 31
26 - 1 = 63
27 - 1 = 127
What do you observe? To the untrained eye, it may seem that all the numbers which are one less than a prime power of two are Mersenne primes.
Most people are quick to assume this fact but it is not true. Take the example of n = 11:
211 - 1 = 2047
While 2047 may look like a prime number, it actually isn’t one because it is divisible by 23.
From this we can conclude that if 2n - 1 is a Mersenne prime, then n is necessarily prime, but if n is a prime number, then 2n - 1 is not necessarily a Mersenne prime.
Comments