What are Perfect Numbers?
Perfect numbers are positive integers which are the sum of its proper divisors (the divisors of a number which exclude the number itself). The study of perfect numbers may go back to the earliest times when numbers first aroused curiosity, so mathematicians aren’t certain of who discovered them.
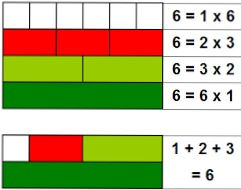
The smallest perfect number is 6 (= 1 + 2 + 3).
Observe this list of perfect numbers:
6 = 1 + 2 + 3
28 = 1 + 2 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
If you scrutinise the factors of these numbers, you may notice that each perfect number has one Mersenne prime factor.
In the case of 6, it is 3.
In the case of 28, it’s 7.
In the case of 496, it’s 31, and so on.
In fact, you can find a perfect number by deriving it from a Mersenne prime:
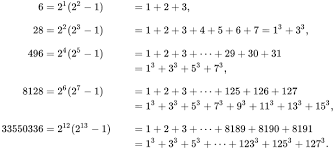
Pick a Mersenne prime M.
Multiply M with M+1 and divide it by two: M(M+1)2
For example:
M=7
M(M+1)2=7(7+1)2=782=28, which is a perfect number.
Let M = 2p - 1, where p is a prime number.
We can derive a perfect number N from M:
N=M(M+1)2=(2p-1)(2p-1+1)2=(2p-1)(2p)2=2p-1(2p-1)
Therefore, for every Mersenne prime 2p-1, there is a perfect number 2p-1(2p-1).
Comments