If you prefer to watch a video on this topic, head over to my youtube channel : https://youtu.be/LpdsraJAt4s.
Integration is one of the most important concepts in Calculus.
There are 2 types of integrating a function:
1) Definite Integration.
2) Indefinite Integration.
Definite Integration is finding the value of an integrand over an interval, while Indefinite Integration is to find the general Anti-Derivative of a function.
For example: ∫x dx = (x^2)/2 + C .
+C represents a constant value. The result of indefinite integration is a family of functions having the same slope at each point, but different 'Y intercepts'.
Let us look at the three functions:
F(x) = (x^2)/2 - 3 , F(x) = (x^2)/2 , F(x) = (x^2)/2 + 3.
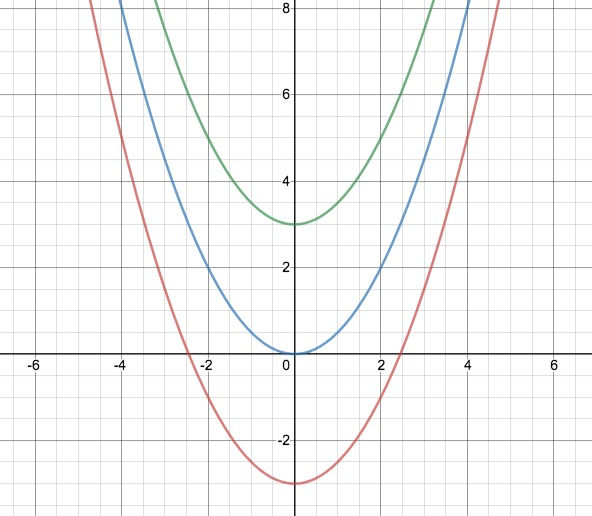
For all three functions, F'(x) = x.
While integrating F'(x) with respect to x, our answer should be F(x).
Without the Constant of Integration +C, the Anti-Derivative would just be (x^2)/2, which would only satisfy F(x) = (x^2)/2. To include all possible solutions which differ by a constant, the +C symbol is added.
The need for the Integration Constant can be displayed well with the trigonometric function F(x) = [tan (x)]^2 .
By the chain rule, F'(x) = 2 tan(x) [sec (x)]^2.
The result of ∫F'(x)dx should ideally give us the original function F(x).
These are 2 of the different ways to solve ∫2 tan(x) [sec (x)]^2 dx .
1) Substitute tan(x) as u.
u = tan(x).
Differentiating with respect to x,
du = [sec (x)]^2 dx.
∫2 tan(x) [sec (x)]^2 dx = 2 ∫u du
2 ∫u du = 2 (u^2)/ 2 = u^2.
Substituting back,
∫2 tan(x) [sec (x)]^2 dx = [tan(x)]^2.
The elementary Anti-Derivative equals the original function F(x) = [tan(x)]^2.
2) Substitute [sec(x)]^2 as u.
u = [sec(x)]^2.
Differentiating with respect to x,
du = 2 tan(x) [sec (x)]^2 dx.
∫2 tan(x) [sec (x)]^2 dx = ∫du
∫du = u.
Substituting back,
∫2 tan(x) [sec (x)]^2 dx = [sec(x)]^2.
Clearly [sec(x)]^2 is not equal to F(x) = [tan(x)]^2.
This error can be avoided through the Constant of Integration.
∫2 tan(x) [sec (x)]^2 dx = [sec(x)]^2 + C'
Can be written as:
[sec(x)]^2 - 1 + C' + 1. { [sec(x)]^2 - 1 = [tan(x)]^2, C'+1 = C as C' is a constant}
= [tan(x)]^2 + C.
The form [sec(x)]^2 + C can be the integral of ∫F'(x)dx where F(x) = [tan(x)]^2.
Therefore, the Constant of Integration is extremely important for Indefinite Integration.